November 03, 2015Long Gong Reading time ~1 minute

Linear Programming

Primal & Dual

1. Form 1:

Primal:

$\begin{align}max.&\quad\mathbf{c}^T \mathbf{x}&\\ s.t.&&\\ &\mathbf{A}\mathbf{x} \le \mathbf{b}&\end{align}$

Dual:

$\begin{align}min.&\quad\mathbf{b}^T\mathbf{x}&\\ s.t.&&\\ &\mathbf{A}^T\mathbf{x}=\mathbf{c}&\\ &\mathbf{x}\ge \mathbf{0}&\end{align}$

November 03, 2015Long Gong Reading time ~5 minutes

Graph Theory

Theory Part

Maximum Matching

Berge’s Theorem [1957]

Given a matching $M$ of a graph $G$ , $M$ is the maximum matching if and only if there is no $M$ -augmenting path in $G$ .

$\Rightarrow$ : if $M$ is the maximum matching, then there would be no $M$ -augmenting path, because otherwise we can increase the size of $M$ .

$\Leftarrow$ : assume there is no $M$ -augmenting path in $G$ , $M$ is not the maximum matching, let $M'$ be the maximum one. Then, let’s analyze $M \Delta M'$ , it is easy to figure out that there are three kinds of subgraphs in $M \Delta M'$ :

1. even-length cycle;
2. even-length path;
3. odd-length path;

Obviously, there has to exist at least one subgraph as Case 3, because otherwise, $M$ would also become the maximum matching. And Case 3 indicates there is a $M$ -augmenting path. Contradiction!! Proof completes!!

Hall’s Condition [1935]

Given a bipartite graph $G(X,Y,E)$ , then there exists a matching $M$ saturates $X$ if and only if for every subset $S\subseteq X$ , $\mid N(S)\mid \ge\mid S\mid$ .

$\Rightarrow$ : if $M$ saturates $X$ , then for every subset $S\subseteq X$ , we have $\mid N(S)\mid \ge \mid \{y:(s,y) \in M, s \in S\}\mid =\mid S\mid$ .

$\Leftarrow$ : we can prove by induction.

Base case, when $\mid X\mid =1$ , obviously the statement holds.

Assume that statement holds when $\mid X\mid \le k - 1$ . When $\mid X\mid =k$ ,

If for every subset $S\subseteq X$ , $N(S)>\mid S\mid$ , then we can remove an arbitrary edge from $G$ obtaining $G'$ . We have, $\mid N(S')\mid \ge \mid S'\mid$ for every subset $S'\subseteq X'$ , therefore, $G'$ has a matching saturates $X'$ . Hence, adding the removed edge, we can get a matching saturating $X$ .
If there exists a subset $S$ such that $\mid N(S)\mid =\mid S\mid$ :

1) if $S$ is a real subset of $X$ , then we have in the subgraph induced by $S$ and $N(S)$ , there exists a matching saturating $S$ , and in the subgraph induced by $X\setminus S$ , there also exists a matching saturating $X\setminus S$ . Therefore, there exists a matching saturating $X$ in $G$ . 2) if $S=X$ is the only subset of $X$ such that $\mid N(S)\mid =\mid S\mid$ , then by Case 1, we can conclude that there exists a matching saturating $X$ .

Here is another proof from Douglas’s Introduction to Graph Theory:

$\Leftarrow$ : This proof focuses on the converse-negative proposition, which means it proves that if $M$ is a maximum matching which does not saturate $X$ , then there exists at least a subset $S\subseteq X$ such that $\mid N(S)\mid <S$ .

Let’s define the set of all the $M$ -alternating paths $P$ which starts from an exposed vertex $u\in X$ , and , we denote $S=P\cap X$ , and $T=P\cap Y$ . We have $T=N(S)$ . And for every vertex $v\in T$ , there exists a vertex $x \in S\setminus \{u\}$ such that $(v,x)\in M$ and any two vertices in $T$ can not share the vertices in $S\setminus \{u\}$ , therefore, $\mid N(S)\mid =\mid T\mid =\mid S\setminus \{u\}\mid <\mid S\mid$ . Proof completes!

Vertex Cover & Matching (Konig’s Theorem)

Given any graph $G$ , the size of the minimum vertex cover $\ge$ the size of the maximum matching, and in bipartite graph, they are equal.

The first part is quite easy. To cover the maximum matching $M$ in $G$ we need exactly $\mid M\mid$ , since no edges in $M$ share common vertices. Therefore, the size of the minimum vertex cover is at least the size of the maximum matching.

In bipartite graph $G(X,Y,E)$ , we have $VC=X \cap M$ is a vertex cover, where $M$ is the maximum matching. Let’s prove by contradiction, if $VC$ is not a vertex cover, then there exists at least an edge $e \in E \setminus M$ whose two end-nodes are both exposed. Therefore, itself forms a $M$ -augmenting path, which contradict with the maximality of $M$ .

Tutte-Berge Formula [1958]

For any Graph $G=(V,E)$ , the size of maximum matching $\nu(G)$ can be expressed as, $\nu(G) = \frac{\mid V\mid }{2} - \max_{U\subseteq V}\frac{o(G\setminus U)-\mid U\mid }{2},$

where $o(G\setminus U)$ is the number of components in $G\setminus U$ with an odd number of vertices.

[hint: induction]

Lemma

Let $G(V,E)$ be a graph such that for each $v \in V$ there is a maximum matching in $G$ that misses $v$ . Then, $\nu(G)=\frac{\mid V\mid -1}{2}$ . In particular, $\mid V\mid$ is odd.

[hint: contradiction]

Maximum Flow

Given a graph $G(V,E)$ , any $s-t$ flow $f$ , and any $s-t$ cut $(S,\bar{S})$ , the value of $f$ $\le$ the capacity of the cut $(S,\bar{S})$ .

[hint: definition & substitution]

According to the definition of a flow, we have, $val(f) = f(s,V) - f(V,s)$

and for any vertex $x$ other than $s$ and $t$ , $f(x,V) - f(V,x) = 0$

Therefore, $\begin{aligned} val(f) &=& f(s,V) - f(V,s)\\ &=& \sum_{i \in S}f(i,V) - \sum{i \in S}f(V,i)\\ &=& f(S,V) - f(V,S)\\ &=& f(S,\bar{S}) + f(S,S) - f(S,S) - f(\bar{S},S)\\ &=& f(S,\bar{S}) - f(\bar{S},S)\\ &\le& cap(S,\bar{S}) \end{aligned}$ where $f(A,B)=\sum_{x\in A,y\in B}f(x,y)$ , and $cap(S,\bar{S}) = \sum_{x\in S,y \in \bar{S}}c(x,y)$ , $c(x,y)$ is the capacity of egde $(x,y)$ .

Lemma: Given a graph $G(V,E)$

Algorithm Part

Hungarian Algorithm for Maximum Cardinality Matching in Bipartite Graph

Hungarian ALgorithm for Maximum Weight Matching (or Assignment Problem)

Faster Bipartite Graph Matching [Hopcroft-Karp Algorithm]

General Graph Matching Algorithm [Edmonds’ Matching ALgorithm or Blossom ALgorithm]

Lemma [GGM 1]: Given a graph $G(V,E)$ , a matching $M$ , and a set of $M$ -exposed vertices $X$ , there exists a polynomial-time (more specifically $O(\mid V\mid +\mid E\mid )$ )) algorithm that either returns a $X-X$ $M$ -alternating walk or reports that there is no such walk.

Lemma [GMM 2]: A shortest $X-X$ $M$ -alternating walk is either a $M$ -augmenting path or a $M$ -flower as a prefix.

Theorem [GMM 1]: Given a graph $G(V,E)$ , a matching $M$ , and an $M$ -blossom $B$ , $M$ is a maximum matching in $G$ iff $M\setminus B$ is the maximum matching in $G\setminus B$ .

Lemma [GMM 3]: Given a graph $G(V,E)$ , a matching $M$ , and an $M$ -blossom $B$ , if there is a $M$ -augmenting path in $G$ , then there exists a $M\setminus B$ -augmenting path in $G\setminus B$ . Particularly, we can find such an augmenting path in $O(\mid E\mid )$ .

November 01, 2015Long Gong Reading time ~2 minutes

Probability

1. Moment Generating Function

Given random variable $X$, its moment generating function is defined as,

$g(t) = E(e^{tX}),$

Property:

$\frac{d^n}{d t^n}g(t)|_{t=0} = \mu_n,$

where $\mu_n$ is the order n moment.

2. Large Deviation

2.1 Markov’s Theorem

If $R$ is a non-negative random variable, then for any $x >0$ , we have,

$\mathbb{P}(R \ge x) \le \frac{\mathbb{E}(R)}{x}.$

proof:

Corollary: If $R$ is a non-negative r.v., then for any $c > 0$ ,

$\mathbb{P}(R \ge c \mathbb{E}(R)) \le \frac{1}{c}.$

Corollary: If $R \le u$ for some $u \in \mathbb{R}$ , then for any $x < u$ ,

$\mathbb{P}(R \le x) \le \frac{u - \mathbb{E}(R)}{u-x}.$

2.2 Chebyshev’s Theorem

For any $x > 0$ and any r.v. $R$ ,

$\mathbb{P}(\mid R - \mathbb{R} \mid \ge x) \le \frac{Var(R)}{x^2}.$

Corollary: For any $c > 0$ ,

$\mathbb{P}(\mid R - \mathbb{R}\mid \ge c \sigma(R)) \le \frac{1}{c^2}.$

Theorem: For any r.v. $R$ ,

$\mathbb{P}(R - \mathbb{E}(R) \ge c \sigma(R)) \le \frac{1}{c^2 + 1}.$ $\mathbb{P}(R - \mathbb{E}(R) \le - c \sigma(R)) \le \frac{1}{c^2 + 1}.$

2.3 Chernoff Bound

Let $T_1, T_2, T_3, ..., T_n$ be any mutually independent r.v.’s such that for any $j \in \{1,2,3,...,n\}$ , $0 \le T_j \le 1$ . Let $T = \sum_{j = 1}^n T_j$ , then for any $c > 1$ ,

$\mathbb{P}(T \ge c \mathbb{E}(T)) \le e^{-z\mathbb{E}(T)}$

where $z = c \ln c + 1 - c > 0$ .

3. Bayes’s Rule

3.1. Discrete Case

$\mathbb{P}_{X|Y}(x\mid y) = \frac{\mathbb{P}_{X,Y}(x,y)}{\mathbb{P}_Y(y)} = \frac{\mathbb{P}_X(x)\mathbb{P}_{Y|X}(y\mid x)}{\mathbb{P}_Y(y)}.$ $\mathbb{P}_Y(y) = \sum_{x}\mathbb{P}_X(x)\mathbb{P}_{Y\mid X}(y \mid x).$

3.2. Continuous Counterpart

$f_{X\mid Y}(x|y)=\frac{f_{X,Y}(x,y)}{f_Y(y)} = \frac{f_X(x)f_{Y|X}(x|y)}{f_Y(y)}.$ $f_Y(y) = \int f_X(x)f_{Y|X}(y|x) dx.$

3.3. Mixed Case

Discrete $X$ , and Continuous $Y$ ,

$\mathbb{P}_{X\mid Y}(x \mid y) = \frac{\mathbb{P}_X(x)f_{Y\mid X}(y\mid x)}{f_Y(y)}.$ $f_Y(y) = \sum_{x} \mathbb{P}_{X}(x) f_{Y\mid X}(y\mid x).$

4. Union Bound

Union bound also known as Boole’s inequality, which is a very simple but useful inequality in probability theory.

Mathematically, let $A_i,i=1,2,...,n$ be a series of events, and $\mathbb{P}(A_i)$ denotes its occurrence probability. The Boole’s inequality says that,

$\mathbb{P}(\cup_{j=1}^{n}A_j) \leq \sum_{j=1}^{n}\mathbb{P}(A_i).$

Which can be considered as a special case of sub-additivity property of Lebesgue measure. I guess the additivity of the probabilities for mutual excursive events (i.e., the countable additivity property of the measure for disjoint measurable sets) which is usually stated in the definition of probability might be better-known to most of us.

August 23, 2015Long Gong Reading time ~1 minute

Approximation Analysis on The Greedy Maximum Bipartite Graph Matching

Recently, I read a paper on semi-streaming algrithm which applied some knowledge about bipartite graph matching. It mentioned a greedy algorithm which could find the maximal matching of a bipartite graph (actually, also applicable to an arbitrary graph), and the size of the maximal matching would be no less than a half of the optimal one, i.e., the maximum matching. In this post, we will learn about this greedy algorithm and the proof of its approximation ratio.

Now, let’s start our journey …

Greedy Algorithm for Maximum Matching

The following code is using python-style.

M = []
flag = {}
for e in E:
	if (e[0] not in flag) and (e[1] not in flag):  
        M.append(e)      
        flag.setdefault(e[0],1)       
        flag.setdefault(e[1],1)

Approximation Ratio Proof

Assume $M’$ is the maximum matching of graph $G(V,E)$, and $M$ is the maximal matching getting from the above greedy algorithm. For any edge $(u,v) \in M’$, we have either $u$ is matched by $M$, or $u$ is matched by $M$. Otherwise, $(u,v)$ should in $M$. Therefore, \(

\geq \frac{1}{2}

M’

\).

Eventually, we proved that the size of the maximal matching getting from the greedy algorithm above, is at least a half of the maximum one.

Note that, this proof is from reference [1].

[1] http://crab.rutgers.edu/~guyk/ex/flow.pdf

August 05, 2015Long Gong Reading time ~1 minute

Solve “Not All Fonts are Embedded” for Latex on Windows

When uploading papers to EDAS, you might encounter a problem which is called as “Not All Fonts are Embedded”. Today, I’ll give you a relatively easy and convenient solution.

Tools

GS x86 for 32-bit Windows

GS x64 for 64-bit Windows

Steps

Download and Install The Proper GS (i.e., GS x86 or GS x64)

Note that, in the following steps, I will assume the GS is installed at “C:/Program Files/gs”!

Change Configuration of WinEdit

Locate the settings of “ps2pdf”: Winedit -> Option -> Exectution Modes -> ps2pdf, as shown in the following figure,
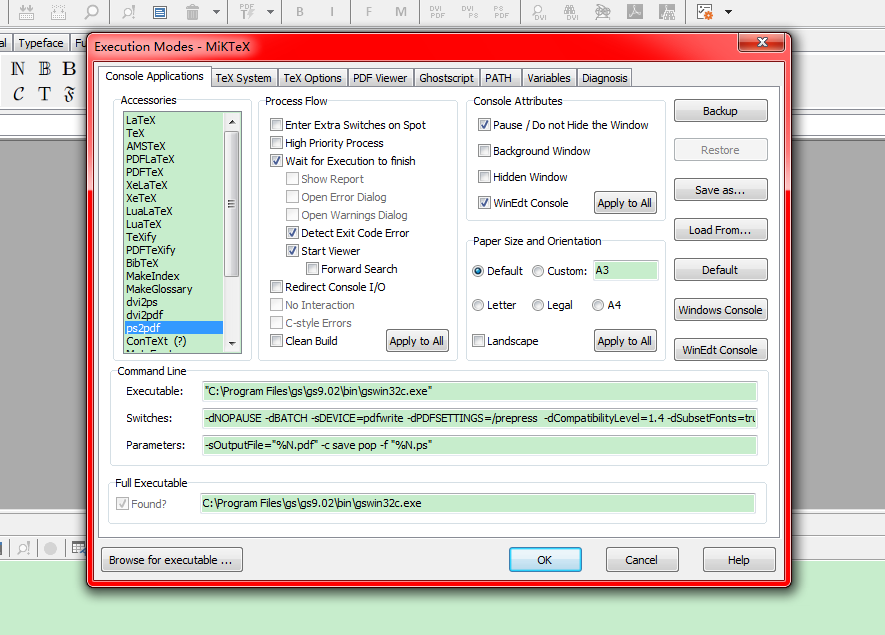
Click “Browse for executable…” at the left-bottom, and select the “gswin32c.exe” at “C:/Program Files/gs/gs9.02/bin/”
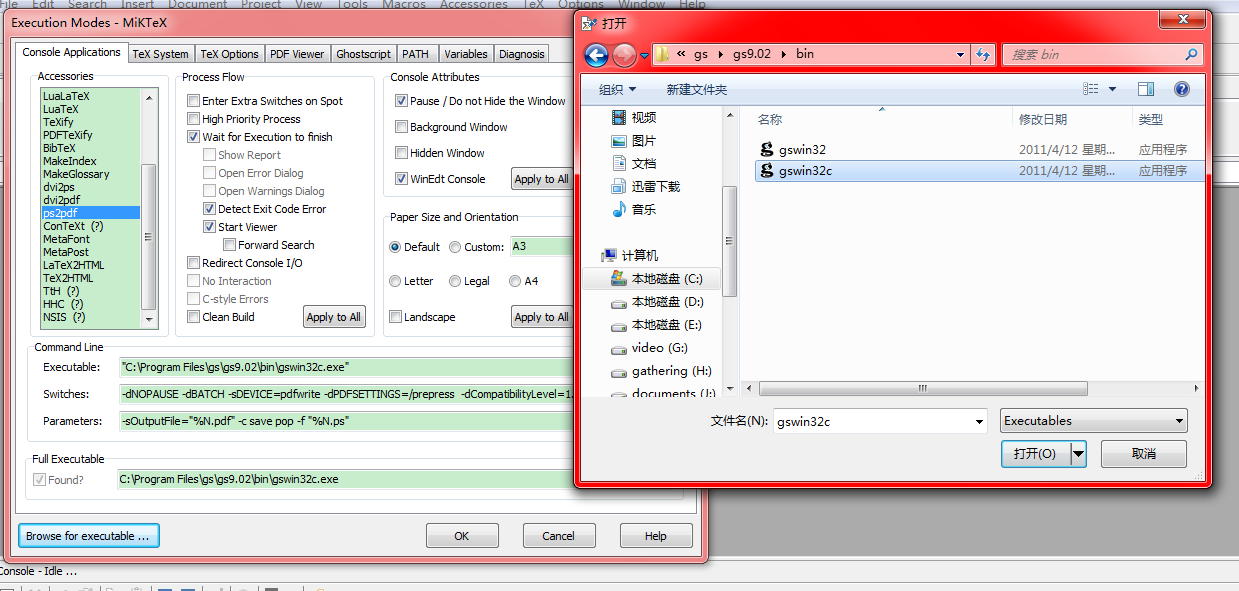
Fill “Switches” entry with the following setting (if it was not empty before filling, then just replace the original one),
```
 -dNOPAUSE -dBATCH -sDEVICE=pdfwrite -dPDFSETTINGS=/prepress  -dCompatibilityLevel=1.4 -dSubsetFonts=true -dEmbedAllFonts=true
```
as shown in the following figure,
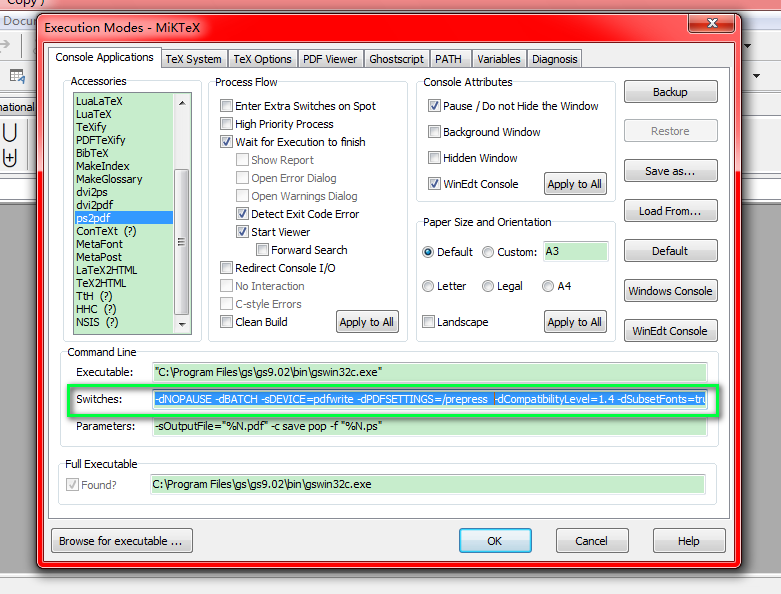
Replace the original setting in “Parameters” entry with the following one,
```
 -sOutputFile="%N.pdf" -c save pop -f "%N.ps"
```
as shown in the following figure,
Click “OK”

Coding Dragon's Blog

Latest Posts