Most content of this post is from the Lecture 2 for Prof. John K. Hunter’s Math 125b and Wikimedia.

Supremum & Infimum of Sets

Definitions

Let $A \subseteq \mathbb{R}$, if $M \in \mathbb{R}$ is the smallest upper bound of $A$, i.e., for any upper bound $M'$ of $A$, we have $M \leq M'$. We call $M$ the supremum of $A$, denoting as $M =\sup A$. If $m \in \mathbb{R}$ is the largest lower bound of $A$, then we call $m$ the infimum of $A$, denoting as $m = \inf A$.

Properties

The supremum or infimum of a set $A$ is unique if exists. Moreover, if both exist, then $\inf A \leq \sup A$.

For $c \geq 0$,
$\sup (cA) = c\sup A,\qquad \inf (cA) = c \inf A$
For $c < 0$,
$\sup (cA) = c \inf A,\qquad \inf (cA) = c\sup A$

Let $A \subseteq B \subseteq \mathbb{R}$, if $\sup A$, $\sup B$ exist, then $\sup A \leq \sup B$. If $\inf A$, $\inf B$ exist, then $\inf A \geq \inf B$.

Let $A,B \subseteq \mathbb{R}$ be non-empty sets, then
$\begin{aligned} \sup (A + B) = \sup A + \sup B,\qquad \inf (A +B)= \inf A + \inf B,\\ \sup (A - B) = \sup A = \inf B,\qquad \inf (A - B) = \inf A - \sup B. \end{aligned}$

Supremum \& Infimum of Functions

Definition

Let $E \subseteq \mathbb{R}$, $f: E \mapsto \mathbb{R}$ is a function, then,
$\sup_{E} f = \sup\{f(x):x \in E\},\qquad \inf_{E} = \inf\{f(x):x \in E\}$

Properties

Let $E \subseteq \mathbb{R}$, $f,g: E \mapsto \mathbb{R}$, if $g$ is bounded from above, then
$\sup_{E} f \leq \sup_{E} g,$
if $f$ is bounded from below, then
$\inf_{E} f \leq \inf_{E} g.$

Let $E \subseteq \mathbb{R}$, $f: E \mapsto \mathbb{R}$ is bounded, $c \in \mathbb{R}$, if $c \geq 0$, then
$\sup_{E} (cf) = c \sup_{E} f,\qquad \inf_E (cf) = c \inf_E f.$
if $c < 0$, then
$\sup_E (cf) = c \inf_E f,\qquad \inf_E (cf) = c \sup_E f.$

Let $E \subseteq \mathbb{R}$, $f,g: E \mapsto \mathbb{R}$ are bounded, then
$\sup_E (f + g) \leq \sup_E f \sup_E g,\,\inf_E (f + g) \geq \inf_E f + \inf_E g.$

Let $E \subseteq \mathbb{R}$, $f,g: E \mapsto \mathbb{R}$ are bounded, then
$\mid \sup_E f - \sup_E g\mid \leq \sup_E \mid f - g \mid,\qquad \mid \inf_E f - \inf_E g\mid \leq \sup_E \mid f - g\mid.$

Definitions

The limit inferior (i.e., liminf) of a sequence $\{x_n\}$ is defined as
$\liminf_{n \rightarrow \infty} x_n = \lim_{n \rightarrow \infty}(\inf_{m \geq n} x_m)$
or
$\liminf_{n \rightarrow \infty} x_n = \sup_{n\geq 0}\inf_{m \geq n} x_m = \sup\{\\inf\{x_m: m \geq n\}:n \geq 0\}.$

Similarly, the limit superior of $\{x_n\}$ is defined by
$\limsup_{n \rightarrow \infty} x_n = \lim_{n \rightarrow \infty}(\sup_{m \geq n} x_m)$
or
$\limsup_{n \rightarrow \infty} x_n = \inf_{n \geq 0}\sup_{m \geq n}x_m = \inf\{\sup\{x_m:m \geq n\}:n \geq 0\}.$

Properties

$\{x_n\}$ converges if and only if
$\limsup_{n \rightarrow \infty} x_n = \liminf_{n \rightarrow \infty}x_n.$

In this post, we will talk about easy ways to draw binary trees.

Binary Trees with Graphviz

This first method is to use the open source Graph Virtualization Software - Graphviz.

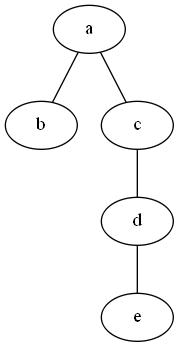
Let’s start an example of drawing a binary tree as shown in the following figure.

First of all, create a file and then type in the following content, and save it as bt.dot.

graph{
    a -- b;
    a -- c;
    c -- d;
    d -- e;
}

Then, open a terminal and use cd command to come to the directory where bt.dot locates, then type in the following command in the terminal, and run it.

dot -Tpng bt.dot -o bt.png

After running the command, you will find bt.png in the same directory as bt.dot. This figure is shown below. (Note that, it seems that Graphviz on Mac does not support png yet, so if you use Mac to go through this example, we can change png to ps or any other types that are supported.)

Of course, Graphviz is much more powerful than that, if you are interested you can refer to the following tutorials:

• Drawing graphs with dot
• Drawing Graphs using Dot and Graphviz

However, from the above simple example, you might already notice that, Graphviz treats left child and right child indistinguishably. So if you want to distinguish between them in your case, it would not be a very good solution. There is no doubt that Graphviz provides you the power to customize the layout or even location of each vertex, however, it would be inconvenient if you have to specify the location for each vertex. And I feel surprised that Graphviz does not provide any easy ways to achieve this goal. On Stackoverflow, someone provides a solution to achieve this goal (I have not tested the solution, I am not sure whether it works or not), but the solution is not perfect.

Binary Tree with Tikz

Tikz-qtree provides a simple solution to draw binary tree in which left and right children are distinguishable.

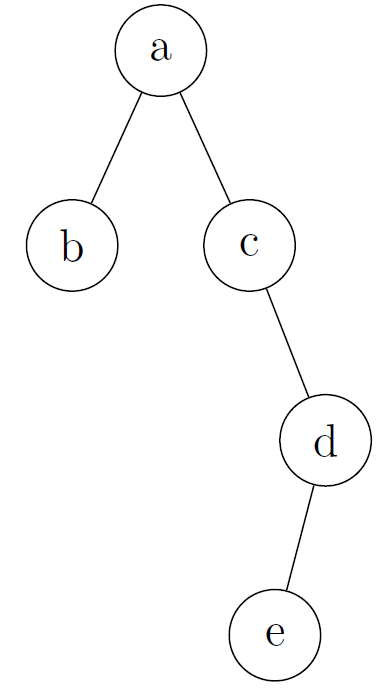
Let’s draw the same binary search as in the above example.

First of all create a file and type in the following content and then save it as bt.tex (note that, the original Latex codes are copied from Stackexcahnge)

\documentclass{article}
\usepackage{tikz-qtree}
\begin{document}
\tikzset{every tree node/.style={minimum width=2em,draw,circle},
         blank/.style={draw=none},
         edge from parent/.style=
         {draw,edge from parent path={(\tikzparentnode) -- (\tikzchildnode)}},
         level distance=1.5cm}
\begin{tikzpicture}
\Tree
[.a     
    [.b ]
    [.c 
    \edge[blank]; \node[blank]{};
    \edge[]; [.d
             \edge[]; {e}
             \edge[blank]; \node[blank]{};
         ]
    ]
]
\end{tikzpicture}
\end{document}

Then, compile bt.tex. The following shows what the binary tree looks like.

The following give some tutorials on how to draw beautiful figures with Tikz:

• TikZ and PGF with a large number of examples
• pgf – Create PostScript and PDF graphics in TEX

Descriptions

System Overview

The above figure shows the overview of our network virtualization system. From it, we can see there are three major modules in our system.

• Virtual Software-Defined Virtual Network Management Module

  A Web GUI for users (or customers) to create and Manage their virtual networks continently.

  Implementation
  Front-end: bootstrap
  Back-end: django

  More details you can refer to the video demo in the following part and my master thesis

• Network Hyper-visor (Extended OpenVirteX, E-OVX for short)

  A openflow-based network hyper-visor supporting for network virtualization

  It is based on OpenVirteX, we did protocol extension on it (i.e., making it support for elastic optical network)

  More details you can refer to the official web of OpenVirteX

• Virtual Network Embedder

  The module to conduct virtual network embedding, which is one of the major challenges in network virtualization

  Motivations to separating it from Network Hyper-visor
  Easily upgrade
  Easily debug

Major Principle

• Topology Virtualization
• Address Virtualization

More details, you can refer to OpenVirteX official web or my master thesis

A Video Demo

The following video shows how a user applies our network virtualization platform to create and manage their virtual networks.

../attachments/demo.mp4

Model details your can refer to my defense ppt and the system part of my master thesis.

Majority Elements (MEs)

Given sequence $A$ of length $N$, the $\theta$-majority elements of $A$ are defined as the elements in $A$ whose occurrences are more than $\theta \cdot N$. For example, if the sequence is $[1,1,2,3,4,1,2,1,2,3,4]$, and $\theta = 0.3$, then the $0.3$-majority elements are $[1]$, since it is the only element whose occurrences are more than $3$.

Methods to Find (MEs)

Basic Hashing Solution

The most direct solution to finding the majority elements would be using a hash table as counters for different elements, and then compare these counters with $\theta \cdot N$. The following give the pseudo codes.

# INPUT: sequence A, and theta
# OUTPUT: majority elements K
N = len(A)
counters = {}
for x in A:
    if counters.has_key(x):
        counters[x] += 1
    else:
        counters[x] = 1

K = []
threshold = int(theta * N)
for key, value in counters.iteritems():
    if value > threshold:
        K.append(key)

Let do some analysis on the above algorithm. First of all, let’s introduce some notations. Let $\Sigma$ be the set of alphabets, and $\Sigma^* = (x_1,x_2,...,x_N)$ be all the possible sequences that can be constructed by using the alphabets from $\Sigma$. Let $A \in \Sigma^*$ be a sequence. And $\mid \Sigma \mid = n$, $\mid A \mid = N$, $0 < \theta \leq 1$, and $m$ is the number of unique elements in $A$.

Obviously, there are at most $\lfloor\frac{1}{\theta}\rfloor$ majority elements in $A$. However, in this basic hashing solution, we need $O(m)$ space, and $O(N)$ time. That is to say, when $m \gg \lfloor\frac{1}{\theta}\rfloor$ (this is the common case that we might encounter in real-life), we would waste a large amount of memory, because amongst all these counters, there are at most $\lfloor\frac{1}{\theta}\rfloor$ would be larger than $\theta\cdot N$. So, could we achieve $O(\frac{1}{\theta})$ space complexity?

Smarter Solution

Actually, it turns out we can achieve $O(\frac{1}{\theta})$ space solution by using similar ideas as Boyer–Moore majority vote algorithm, which is an space-efficient linear-time algorithm to find the $0.5$ majority element in an sequence.

This method was first proposed by Richard M. Karp, Scott Shenker, and Christos H. Papadimitriou in @KarpShenkerPapadimitriou2003 and Erik D. Demaine et al in DemaineLopezOrtizMunro2002. It works as follows. It increases the number of counters as encountering new elements when passing through the sequence, and whenever the number of counters reaches $\lceil \frac{1}{\theta}\rceil$, it starts to decrease all the counters by one, and if any counter reaches $0$, removing it. Therefore, it can guarantee that there are at most $\lceil \frac{1}{\theta}\rceil$ counters. It is easy to figure out if an element has occurrences more than $\theta \cdot N$, its counter must survive. Therefore, if we define $S$ as the set of elements whose counters survived after passing through all the elements in the sequence. The the set of majority elements must be a subset of $S$. Therefore, by passing through the sequence again checking whether the occurrences of elements in $S$ exceed $\theta \cdot N$, we can obtain all the majority elements.

The following provides that pseudo codes.

# INPUT/OUTPUT the same as before

N = len(A)
counters = {}

M = int(1.0 / theta)
for x in A:
    if counters.has_key(x):
        counters[x] += 1
    else:
        counters[x] = 1

    if len(counters) > M:
        for key in counters:
            counters[key] -= 1
            if counters[key] == 0:
                del counters[key]

# check all survived keys in counters
for key in counters:
    counters[key] = 0

for x in A:
    if counters.has_key(x):
        counters[x] += 1

K = []
threshold = int(theta * N)
for key in counters:
    if counters[key] > threshold:
        K.append(key)

References